
| Existence |
|---|
| Duality |
|---|
| Symmetry |
|---|
| The Kepler-Poinsot Regular Star-Polyhedra |
|---|
| An Atlas of Regular Polyhedra |
|---|
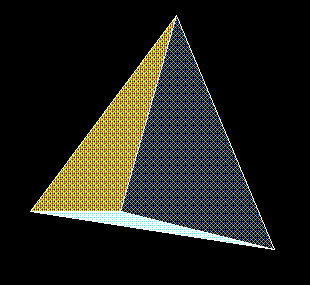 Choose any four
points in three-dimensional space that don’t all lie in the
same plane and they will be the corners of a tetrahedron: a
polyhedron with just four faces. This is the simplest possible
kind of polyhedron, so it is often called a three-dimensional
simplex. If the six edges, representing the distances
between the six distinct pairs of the four points, are all of
equal length, then the tetrahedron automatically is regular. Its
faces, which correspond to the four different ways to select any
three of the four points, become equilateral triangles; the
regular tetrahedron is the particular regular polyhedron that has
three equilateral triangles at every corner. (If the edges are
not all equal, the tetrahedron is irregular. There are several
different kinds of irregular tetrahedra, such as triangular
pyramids, sphenoids, disphenoids, and orthoschemes, but they fall
outside the scope of this page.) In Plato’s cosmology, the
regular tetrahedron was associated with the element
Fire.
Choose any four
points in three-dimensional space that don’t all lie in the
same plane and they will be the corners of a tetrahedron: a
polyhedron with just four faces. This is the simplest possible
kind of polyhedron, so it is often called a three-dimensional
simplex. If the six edges, representing the distances
between the six distinct pairs of the four points, are all of
equal length, then the tetrahedron automatically is regular. Its
faces, which correspond to the four different ways to select any
three of the four points, become equilateral triangles; the
regular tetrahedron is the particular regular polyhedron that has
three equilateral triangles at every corner. (If the edges are
not all equal, the tetrahedron is irregular. There are several
different kinds of irregular tetrahedra, such as triangular
pyramids, sphenoids, disphenoids, and orthoschemes, but they fall
outside the scope of this page.) In Plato’s cosmology, the
regular tetrahedron was associated with the element
Fire. Self-dual
polyhedra are few and far between, but even rarer are figures for
which the duality operation is also a symmetry. The regular
tetrahedron is self-dual, but when it is dualized, it inverts, so
that the corners of the dual are located where the faces of the
original were, and vice versa. The Stella Octangula, which
is a compound of two regular tetrahedra in dual position, is not
just self-dual but remains unchanged after dualization.
Dualization simply exchanges the two tetrahedra; it is a
central inversion.
Self-dual
polyhedra are few and far between, but even rarer are figures for
which the duality operation is also a symmetry. The regular
tetrahedron is self-dual, but when it is dualized, it inverts, so
that the corners of the dual are located where the faces of the
original were, and vice versa. The Stella Octangula, which
is a compound of two regular tetrahedra in dual position, is not
just self-dual but remains unchanged after dualization.
Dualization simply exchanges the two tetrahedra; it is a
central inversion. Having
seen the vertices of a cube in the Stella Octangula, we now meet
the cube itself. This is by far the most familiar of the regular
polyhedra, being the fundamental solid of all architecture and
the only regular polyhedron that can be tiled by itself to fill
three-space. A cube of unit edge is defined as the unit of
volume, and all other volumes are measured by the number of unit
cubes they can contain. For this reason, it is also known as the
three-dimensional measure polytope. Three squares come
together at each vertex, for a total of six squares. This gives
us the cube’s formal Greek name, regular hexahedron.
The cube is also the Archimedean square prism and, if
stood on a corner, the triangular antibipyramid. In
Plato’s cosmology, the cube was associated with the element
Earth.
Having
seen the vertices of a cube in the Stella Octangula, we now meet
the cube itself. This is by far the most familiar of the regular
polyhedra, being the fundamental solid of all architecture and
the only regular polyhedron that can be tiled by itself to fill
three-space. A cube of unit edge is defined as the unit of
volume, and all other volumes are measured by the number of unit
cubes they can contain. For this reason, it is also known as the
three-dimensional measure polytope. Three squares come
together at each vertex, for a total of six squares. This gives
us the cube’s formal Greek name, regular hexahedron.
The cube is also the Archimedean square prism and, if
stood on a corner, the triangular antibipyramid. In
Plato’s cosmology, the cube was associated with the element
Earth.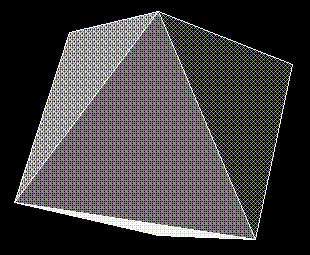 The dual of the cube is the regular octahedron, which
has four equilateral triangles meeting at each of its six
vertices. One may think of this polyhedron as two square pyramids
with equilateral triangles for lateral faces joined base to base,
so that it is the Archimedean square bipyramid. Or one may
think of it as a pair of equilateral triangles in parallel planes
rotated 60° out of alignment with each other, connected by a
band of six equilateral triangles between them. This makes it the
Archimedean triangular antiprism. As the dual of the cube,
or three-dimensional measure polytope and orthotope, it is also
known as a three-dimensional cross polytope and as a
three-dimensional orthoplex, respectively. There are many
kinds of irregular octahedra—polyhedra with eight
faces—some very pretty, but only one of them is regular. In
Plato’s cosmology, the regular octahedron was associated
with the element Air.
The dual of the cube is the regular octahedron, which
has four equilateral triangles meeting at each of its six
vertices. One may think of this polyhedron as two square pyramids
with equilateral triangles for lateral faces joined base to base,
so that it is the Archimedean square bipyramid. Or one may
think of it as a pair of equilateral triangles in parallel planes
rotated 60° out of alignment with each other, connected by a
band of six equilateral triangles between them. This makes it the
Archimedean triangular antiprism. As the dual of the cube,
or three-dimensional measure polytope and orthotope, it is also
known as a three-dimensional cross polytope and as a
three-dimensional orthoplex, respectively. There are many
kinds of irregular octahedra—polyhedra with eight
faces—some very pretty, but only one of them is regular. In
Plato’s cosmology, the regular octahedron was associated
with the element Air. Just as two
tetrahedra can be put together concentrically in “dual
position” to produce a Stella Octangula, so can the
octahedron and cube be compounded into a figure that vividly
demonstrates their duality. In the compound, each corner of the
octahedron is centered above a face of the cube, and vice
versa. Because the two polyhedra have the same midradius (the
distance from the center to the midpoint of any edge), each edge
of the octahedron perpendicularly bisects a corresponding edge of
the cube, and vice versa. The compound is not regular,
because it comprises two different polyhedra and has two
different kinds of corners; but it is nevertheless very
symmetric. The polyhedron common to both solids has six squares
and eight triangles for faces and is called a
cuboctahedron. The smallest polyhedron that encloses the
two polyhedra has twelve identical faces, each a rhombus whose
diagonals are the perpendicularly bisecting edge-pairs. Not
surprisingly, it is the dual of the cuboctahedron, and it is
called a rhombic dodecahedron (to distinguish it from the
regular dodecahedron, whose twelve faces are
pentagons).
Just as two
tetrahedra can be put together concentrically in “dual
position” to produce a Stella Octangula, so can the
octahedron and cube be compounded into a figure that vividly
demonstrates their duality. In the compound, each corner of the
octahedron is centered above a face of the cube, and vice
versa. Because the two polyhedra have the same midradius (the
distance from the center to the midpoint of any edge), each edge
of the octahedron perpendicularly bisects a corresponding edge of
the cube, and vice versa. The compound is not regular,
because it comprises two different polyhedra and has two
different kinds of corners; but it is nevertheless very
symmetric. The polyhedron common to both solids has six squares
and eight triangles for faces and is called a
cuboctahedron. The smallest polyhedron that encloses the
two polyhedra has twelve identical faces, each a rhombus whose
diagonals are the perpendicularly bisecting edge-pairs. Not
surprisingly, it is the dual of the cuboctahedron, and it is
called a rhombic dodecahedron (to distinguish it from the
regular dodecahedron, whose twelve faces are
pentagons).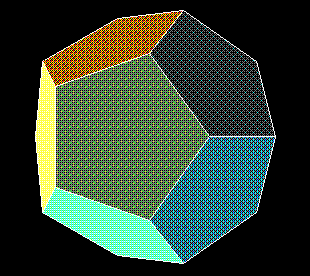 The high order of symmetry and the appearance
of fivefold rotational axes in the “pentagonal
polyhedra” make them the most elegant of the regular solids.
In the dodecahedron, three regular pentagons meet at each vertex,
there being a total of twelve pentagons in the polyhedron. Plato
had a difficult time fitting this figure into his cosmology.
Having assigned the classical Four Elements to the other four
regular polyhedra, he decided the dodecahedron should be
associated with a “fifth element,” or
quintessence: the universal Æther.
The high order of symmetry and the appearance
of fivefold rotational axes in the “pentagonal
polyhedra” make them the most elegant of the regular solids.
In the dodecahedron, three regular pentagons meet at each vertex,
there being a total of twelve pentagons in the polyhedron. Plato
had a difficult time fitting this figure into his cosmology.
Having assigned the classical Four Elements to the other four
regular polyhedra, he decided the dodecahedron should be
associated with a “fifth element,” or
quintessence: the universal Æther.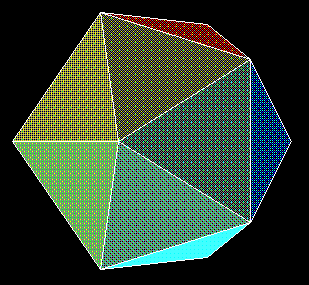 The regular
polyhedron with five equilateral triangles at each corner
requires 20 triangles for its assembly, so it is called an
icosahedron. It is the dual of the regular dodecahedron, and it
has twelve corners and 30 edges. Unlike the tetrahedron, cube,
and dodecahedron, but like the octahedron, the icosahedron
remains “floppy” until the last face is to be fitted
in. This is because the first three polyhedra have all trivalent
vertices (meaning three faces come together at each corner),
which automatically makes the corners rigid, like any triangle.
The octahedron and icosahedron, however, have more than three
faces at a corner, and this allows them to flex until all but the
very last face is in place. One may remove as many as four
strategically placed triangles of the 20 of an icosahedron and
the resulting structure will still remain rigid: choose the four
so that only one of them is at each vertex. The icosahedron is
just as pretty as the regular dodecahedron, by virtue of its
threefold and fivefold symmetry axes. In Plato’s cosmology,
the regular icosahedron was associated with the element
Water.
The regular
polyhedron with five equilateral triangles at each corner
requires 20 triangles for its assembly, so it is called an
icosahedron. It is the dual of the regular dodecahedron, and it
has twelve corners and 30 edges. Unlike the tetrahedron, cube,
and dodecahedron, but like the octahedron, the icosahedron
remains “floppy” until the last face is to be fitted
in. This is because the first three polyhedra have all trivalent
vertices (meaning three faces come together at each corner),
which automatically makes the corners rigid, like any triangle.
The octahedron and icosahedron, however, have more than three
faces at a corner, and this allows them to flex until all but the
very last face is in place. One may remove as many as four
strategically placed triangles of the 20 of an icosahedron and
the resulting structure will still remain rigid: choose the four
so that only one of them is at each vertex. The icosahedron is
just as pretty as the regular dodecahedron, by virtue of its
threefold and fivefold symmetry axes. In Plato’s cosmology,
the regular icosahedron was associated with the element
Water.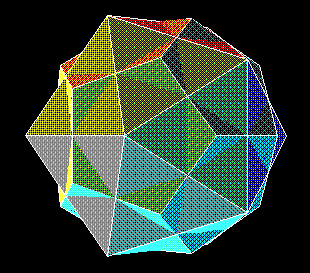 Like two
tetrahedra and the cube and octahedron, the regular icosahedron
and dodecahedron can be placed concentrically in “dual
position.” This makes a pretty, symmetric compound in which
the vertices of either polyhedron lie above the centers of the
faces of the other, and the edges of either polyhedron
perpendicularly bisect the edges of the other. The inner
polyhedron common to both solids has twelve pentagons and 20
triangles for faces and is called an icosidodecahedron.
The smallest polyhedron that encloses the two polyhedra has 30
identical faces, each a rhombus whose diagonals are the
perpendicularly bisecting edge-pairs. It is the dual of the
icosidodecahedron and is called a rhombic triacontahedron.
These figures fall neatly into the pattern begun with the Stella
Octangula and the compound of octahedron and cube.
Like two
tetrahedra and the cube and octahedron, the regular icosahedron
and dodecahedron can be placed concentrically in “dual
position.” This makes a pretty, symmetric compound in which
the vertices of either polyhedron lie above the centers of the
faces of the other, and the edges of either polyhedron
perpendicularly bisect the edges of the other. The inner
polyhedron common to both solids has twelve pentagons and 20
triangles for faces and is called an icosidodecahedron.
The smallest polyhedron that encloses the two polyhedra has 30
identical faces, each a rhombus whose diagonals are the
perpendicularly bisecting edge-pairs. It is the dual of the
icosidodecahedron and is called a rhombic triacontahedron.
These figures fall neatly into the pattern begun with the Stella
Octangula and the compound of octahedron and cube. The pentagram, or
regular five-pointed star, was known to the Pythagoreans, who
thought it had mystic medical significance but failed to see it
as a regular polygon. The 14th-century
British mathematician Thomas Bradwardine (Bredwardin, or
Bradwardinus) first studied star-polygons systematically and
realized that there is a regular p-pointed star for every
p > 4 and d such that 1 < d < p/2 and
the fraction p/d is in lowest
terms. The pentagram is the simplest regular star-polygon, with
p = 5 and d = 2. There is no regular six-pointed
star, only a six-pointed compound of two equilateral triangles,
the Star of David. There are two seven-pointed stars (or
heptagrams), one eight-pointed star (or octagram),
two nine-pointed stars (or enneagrams), one ten-pointed
star (or decagram), and so forth. The Schläfli symbol
for a p-gon, {p}, extends readily to star-polygons
by using fractions: {p/d}
denotes the star-polygon whose edges cycle d times around
the center before returning to the starting vertex. It is when
the fraction p/d is not in
lowest terms that a regular compound polygon
results.
The pentagram, or
regular five-pointed star, was known to the Pythagoreans, who
thought it had mystic medical significance but failed to see it
as a regular polygon. The 14th-century
British mathematician Thomas Bradwardine (Bredwardin, or
Bradwardinus) first studied star-polygons systematically and
realized that there is a regular p-pointed star for every
p > 4 and d such that 1 < d < p/2 and
the fraction p/d is in lowest
terms. The pentagram is the simplest regular star-polygon, with
p = 5 and d = 2. There is no regular six-pointed
star, only a six-pointed compound of two equilateral triangles,
the Star of David. There are two seven-pointed stars (or
heptagrams), one eight-pointed star (or octagram),
two nine-pointed stars (or enneagrams), one ten-pointed
star (or decagram), and so forth. The Schläfli symbol
for a p-gon, {p}, extends readily to star-polygons
by using fractions: {p/d}
denotes the star-polygon whose edges cycle d times around
the center before returning to the starting vertex. It is when
the fraction p/d is not in
lowest terms that a regular compound polygon
results. The twelve pentagrammatic faces of a small
stellated dodecahedron may be extended until they meet the
extensions of other faces, just as the edges of a dodecahedron
are extended to meet other edge-extensions to create the small
stellated dodecahedron. The polyhedron that results is the
great dodecahedron. Although the twelve vertices of the
original small stellated dodecahedron remain, the 30 original
edges are lost; they simply become the lines of intersection
between the faces of the great dodecahedron. These faces are
twelve regular pentagons, specifically the pentagons that
circumscribe the twelve pentagrams of the small stellated
dodecahedron. The 30 new edges formed by these pentagons are also
the edges of the circumscribing icosahedron, which shows that the
great dodecahedron is also a faceted icosahedron.
The twelve pentagrammatic faces of a small
stellated dodecahedron may be extended until they meet the
extensions of other faces, just as the edges of a dodecahedron
are extended to meet other edge-extensions to create the small
stellated dodecahedron. The polyhedron that results is the
great dodecahedron. Although the twelve vertices of the
original small stellated dodecahedron remain, the 30 original
edges are lost; they simply become the lines of intersection
between the faces of the great dodecahedron. These faces are
twelve regular pentagons, specifically the pentagons that
circumscribe the twelve pentagrams of the small stellated
dodecahedron. The 30 new edges formed by these pentagons are also
the edges of the circumscribing icosahedron, which shows that the
great dodecahedron is also a faceted icosahedron. It is possible to place a
small stellated dodecahedron and a great dodecahedron in
“dual position,” but the resulting figure hides the
great dodecahedron inside the small stellated dodecahedron
completely, so a paper model is not particularly enlightening!
One might, however, construct a beautiful model of this compound
with the small stellated dodecahedron in transparent plastic. The
picture here shows the two polyhedra in proper position, with the
small stellated dodecahedron rendered semitransparent. It was
drawn by my polyhedron-pal Russell Towle using his POV-ray
system, because Mathematica 2.1 cannot draw transparent
faces. The polyhedron common to both star-polytopes in the
compound is a dodecadodecahedron; its
faces are twelve pentagons and twelve pentagrams. It is
self-conjugate. Its dual is a star-polyhedron with 30 narrow
rhombic faces called a medial rhombic triacontahedron; the
diagonals of its rhombic faces are the edges of the two dually
placed regular star-polyhedra. The larger diagonal (edge of the
small stellated dodecahedron) is tau+1 =
tau2 times the length of the
smaller diagonal (edge of the great dodecahedron), where
tau is the golden ratio, [sqrt(5)+1]/2.
It is possible to place a
small stellated dodecahedron and a great dodecahedron in
“dual position,” but the resulting figure hides the
great dodecahedron inside the small stellated dodecahedron
completely, so a paper model is not particularly enlightening!
One might, however, construct a beautiful model of this compound
with the small stellated dodecahedron in transparent plastic. The
picture here shows the two polyhedra in proper position, with the
small stellated dodecahedron rendered semitransparent. It was
drawn by my polyhedron-pal Russell Towle using his POV-ray
system, because Mathematica 2.1 cannot draw transparent
faces. The polyhedron common to both star-polytopes in the
compound is a dodecadodecahedron; its
faces are twelve pentagons and twelve pentagrams. It is
self-conjugate. Its dual is a star-polyhedron with 30 narrow
rhombic faces called a medial rhombic triacontahedron; the
diagonals of its rhombic faces are the edges of the two dually
placed regular star-polyhedra. The larger diagonal (edge of the
small stellated dodecahedron) is tau+1 =
tau2 times the length of the
smaller diagonal (edge of the great dodecahedron), where
tau is the golden ratio, [sqrt(5)+1]/2. If the edges of a great
dodecahedron are extended until they meet other edges, the twelve
pentagons stellate into pentagrams, and another regular
star-polyhedron appears: the great stellated dodecahedron.
This star-polyhedron has twelve interpenetrating pentagrammatic
faces meeting three around a vertex, so it has 20 vertices. Its
30 edges are, of course, merely extensions of the 30 edges of the
underlying great dodecahedron. Since each vertex lies directly
above one of the 20 trihedral dimples of the underlying great
dodecahedron, they must be the vertices of a circumscribing
regular dodecahedron. The great stellated dodecahedron is the
only regular polyhedron that is a faceting of the regular
dodecahedron; the other three are all facetings of the regular
icosahedron. It is the dual of the great icosahedron and the
conjugate of the regular dodecahedron. Because of its derivation
by stellation of the great dodecahedron, we can also call it a
stellated great dodecahedron.
If the edges of a great
dodecahedron are extended until they meet other edges, the twelve
pentagons stellate into pentagrams, and another regular
star-polyhedron appears: the great stellated dodecahedron.
This star-polyhedron has twelve interpenetrating pentagrammatic
faces meeting three around a vertex, so it has 20 vertices. Its
30 edges are, of course, merely extensions of the 30 edges of the
underlying great dodecahedron. Since each vertex lies directly
above one of the 20 trihedral dimples of the underlying great
dodecahedron, they must be the vertices of a circumscribing
regular dodecahedron. The great stellated dodecahedron is the
only regular polyhedron that is a faceting of the regular
dodecahedron; the other three are all facetings of the regular
icosahedron. It is the dual of the great icosahedron and the
conjugate of the regular dodecahedron. Because of its derivation
by stellation of the great dodecahedron, we can also call it a
stellated great dodecahedron. The great icosahedron is the dual of the great
stellated dodecahedron. Its faces are 20 triangles: large faces
almost as big as the whole polyhedron, which pass through one
another quite intricately. Deep inside the polyhedron, the
face-planes bound a tiny central icosahedron. The great
icosahedron is the conjugate of the regular icosahedron. Whereas
the five triangles at every vertex of a regular icosahedron cycle
around each vertex once in a pentagonal vertex figure, the five
triangles at every vertex of a great icosahedron cycle around
each vertex twice in a pentagrammatic vertex figure. Just as the
vertices and edges of a regular icosahedron belong to an
inscribed great dodecahedron, so do the edges and vertices of a
great icosahedron belong to a circumscribed small stellated
dodecahedron, which is the conjugate of a great
dodecahedron.
The great icosahedron is the dual of the great
stellated dodecahedron. Its faces are 20 triangles: large faces
almost as big as the whole polyhedron, which pass through one
another quite intricately. Deep inside the polyhedron, the
face-planes bound a tiny central icosahedron. The great
icosahedron is the conjugate of the regular icosahedron. Whereas
the five triangles at every vertex of a regular icosahedron cycle
around each vertex once in a pentagonal vertex figure, the five
triangles at every vertex of a great icosahedron cycle around
each vertex twice in a pentagrammatic vertex figure. Just as the
vertices and edges of a regular icosahedron belong to an
inscribed great dodecahedron, so do the edges and vertices of a
great icosahedron belong to a circumscribed small stellated
dodecahedron, which is the conjugate of a great
dodecahedron. Now use either
short edge of the isosceles triangle as the short edge of the
slender scalene triangle. The angles of the scalene triangle are
22.238756...°, 82.238756...°, and 75.522488...°. The
short edge is opposite the smallest angle, of course, so lay out
the triangle so that the larger two angles are at the short edge.
Check the triangle by measuring the length of the edge opposite
the 75+° angle: it should be very close to 3.236067... inches
long for a 14.4-inch-diameter model. This edgelet is either of
the two longer end sections of each true edge of the model and
will, one hopes, line up straight with the base of an
isosceles-triangular facelet when the model is
assembled.
Now use either
short edge of the isosceles triangle as the short edge of the
slender scalene triangle. The angles of the scalene triangle are
22.238756...°, 82.238756...°, and 75.522488...°. The
short edge is opposite the smallest angle, of course, so lay out
the triangle so that the larger two angles are at the short edge.
Check the triangle by measuring the length of the edge opposite
the 75+° angle: it should be very close to 3.236067... inches
long for a 14.4-inch-diameter model. This edgelet is either of
the two longer end sections of each true edge of the model and
will, one hopes, line up straight with the base of an
isosceles-triangular facelet when the model is
assembled.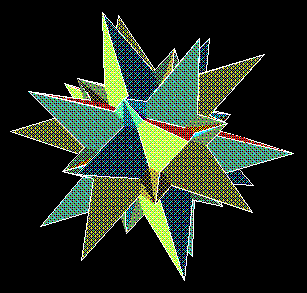 The compound of the
great icosahedron and its dual great stellated dodecahedron in
“dual position” has little fluted-pyramidal
points—small pieces of the great icosahedron—emerging
from each of the twelve reentrant vertices of a big great
stellated dodecahedron: perhaps not a particularly interesting
figure, since so much of the great icosahedron is hidden. But
with its 32 points of two different sizes, it’s pretty to
look at. The figure common to both star-polyhedra in the compound
is the great icosidodecahedron; its
dual is the great rhombic triacontahedron, whose 30
interpenetrating rhombic faces contain the edges of both regular
star-polyhedra as their diagonals. The face of the great rhombic
triacontahedron is a rhombus of the same shape as the face of the
ordinary rhombic triacontahedron.
The compound of the
great icosahedron and its dual great stellated dodecahedron in
“dual position” has little fluted-pyramidal
points—small pieces of the great icosahedron—emerging
from each of the twelve reentrant vertices of a big great
stellated dodecahedron: perhaps not a particularly interesting
figure, since so much of the great icosahedron is hidden. But
with its 32 points of two different sizes, it’s pretty to
look at. The figure common to both star-polyhedra in the compound
is the great icosidodecahedron; its
dual is the great rhombic triacontahedron, whose 30
interpenetrating rhombic faces contain the edges of both regular
star-polyhedra as their diagonals. The face of the great rhombic
triacontahedron is a rhombus of the same shape as the face of the
ordinary rhombic triacontahedron.| Polyhedral Properties |
|---|
| The Regular Polyhedra | ||||||||
|---|---|---|---|---|---|---|---|---|
| Name & symbols | V | E | Faces | Dihedral angle | Symmetry group | Circumradius edge=2 | Midradius edge=2 | Inradius edge=2 |
| Regular tetrahedron {3,3} 3 | 2 3 | 4 | 6 | 4 triangles | 2arctan[sqrt(2)/2] =70.528779...° | [3,3], of order 24 | sqrt(3/2) =1.224744... | sqrt(2)/2 =0.707106... | sqrt(1/6) =0.408248... |
| Cube {4,3} 3 | 2 4 | 8 | 12 | 6 squares | 90° | [3,4], of order 48 | sqrt(3) =1.732050... | sqrt(2) =1.414213... | 1 |
| Regular
octahedron {3,4} 4 | 2 3 | 6 | 12 | 8 triangles | 2arctan[sqrt(2)] =109.471220...° | [3,4], of order 48 | sqrt(2) =1.414213... | 1 | sqrt(2/3) =0.816496... |
| Regular
dodecahedron {5,3} 3 | 2 5 | 20 | 30 | 12 pentagons | 2arctan(T) =116.565051...° | [3,5], of order 120 | Tsqrt(3)
=2.802517... | T+1 =2.618033... | (T+1)/sqrt(3-T) =2.227032... |
| Regular
icosahedron {3,5} 5 | 2 3 | 12 | 30 | 20 triangles | 2arctan(T+1) =138.189685...° | [3,5], of order 120 | sqrt(T+2) =1.902113... | T =1.618033... | sqrt(T+2/3) =1.511522... |
| Name & symbols | V | E | Faces | Dihedral angle | Symmetry group | Circumradius edge=2 | Midradius edge=2 | Inradius edge=2 |
| Small stellated
dodecahedron {5/2,5} 5 | 2 5/2 | 12 | 30 | 12 pentagrams | 2arctan(T) =116.565051...° | [3,5], of order 120 | sqrt(T+2)/T =1.175570... | T-1 =0.618033... | (T-1)/sqrt(3-T) =0.525731... |
| Great
dodecahedron {5,5/2} 5/2 | 2 5 | 12 | 30 | 12 pentagons | 2arctan(T-1) =63.434948...° | [3,5], of order 120 | sqrt(T+2)
=1.902113... | T =1.618033... | 1/sqrt(3-T) =0.850650... |
| Great
stellated dodecahedron {5/2,3} 3 | 2 5/2 | 20 | 30 | 12 pentagrams | 2arctan(T-1) =63.434948...° | [3,5], of order 120 | sqrt(3)/T =1.070466... | 1/(T+1) =0.381966... | 1/[sqrt(3-T)]T3 =0.200811... |
| Great
icosahedron {3,5/2} 5/2 | 2 3 | 12 | 30 | 20 triangles | 2arctan[1/(T+1)] =41.810314...° | [3,5], of order 120 | sqrt(T+2)/T =1.175570... | T-1 =0.618033... | sqrt(T+2/3)/T4 =0.220528... |